59.螺旋矩阵 II

真的是一点思路都没有啊,他开头

int** generateMatrix(int n, int* returnSize, int** returnColumnSizes)

就给我看蒙蔽了

int* returnSize 和 int** returnColumnSizes 这两个参数通常用于返回函数的输出信息，尤其是在 C 语言中，函数可以返回多个值时需要用到它们。具体来说：

int* returnSize：
这个指针用于返回生成的矩阵的行数。在你的函数中，矩阵是 n x n 的，所以在计算完毕后，将 *returnSize 设置为 n。调用者可以通过这个指针获取矩阵的行数。

int** returnColumnSizes：
这个指针用于返回一个数组，数组的每个元素表示对应行的列数。对于一个 n x n 的矩阵，每一行的列数都是 n，所以你会为这个指针分配大小为 n 的数组，并将每个元素都设置为 n。调用者可以通过这个指针知道矩阵的每一行有多少列。

不直接用int这俩玩意是为了在函数内部能够修改他们,对于下面用**是因为他要表示每一行的列数,其实并没有什么用

C语言小知识:

• 接下来这里是重点:

• 在 C 语言中，动态分配的二维数组需要为每一行单独分配内存。

  也就是说,我们不但需要

  int ** matrix=(int **)malloc(n*sizeof(int *));

  还需要在底下补上

  for(int i=0;i<n;i++)
      {
          matrix[i]=(int*)malloc(n*sizeof(int));
      }

  才能使C语言中二维数组正常运行

• 当我们在函数外部定义一个二维数组时是不需要再单独分配空间的

  int a[3][3] = {
      {1, 2, 3},
      {4, 5, 6},
      {7, 8, 9}
  };

  这样子是因为编译器在编译时已经为整个数组分配了足够的内存。

思路:

就是把1~n*n存到二维数组里,我们只要考虑怎样螺旋问题就能迎刃而解

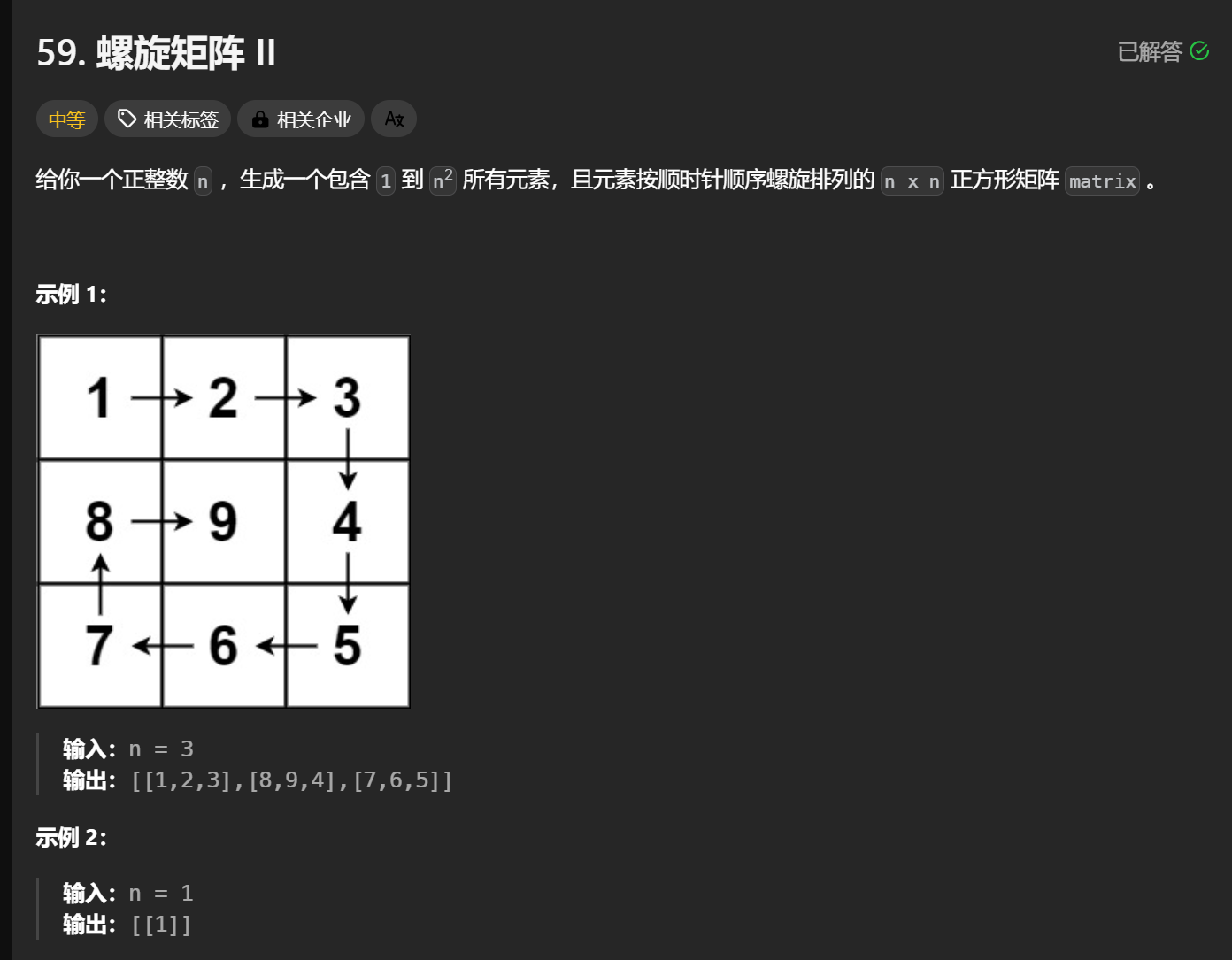
先来一个简单的3*3

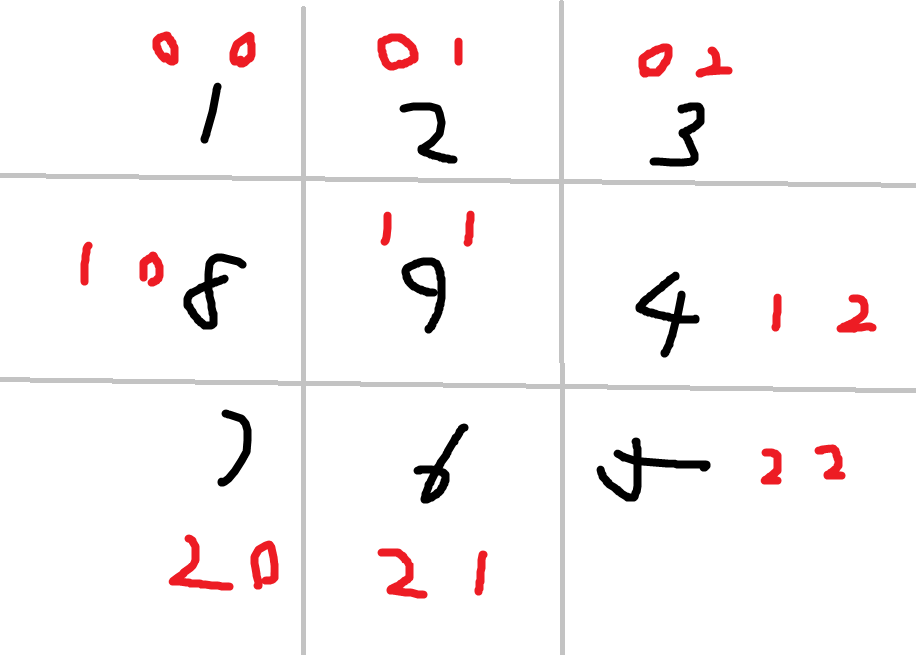
接着是一个4*4

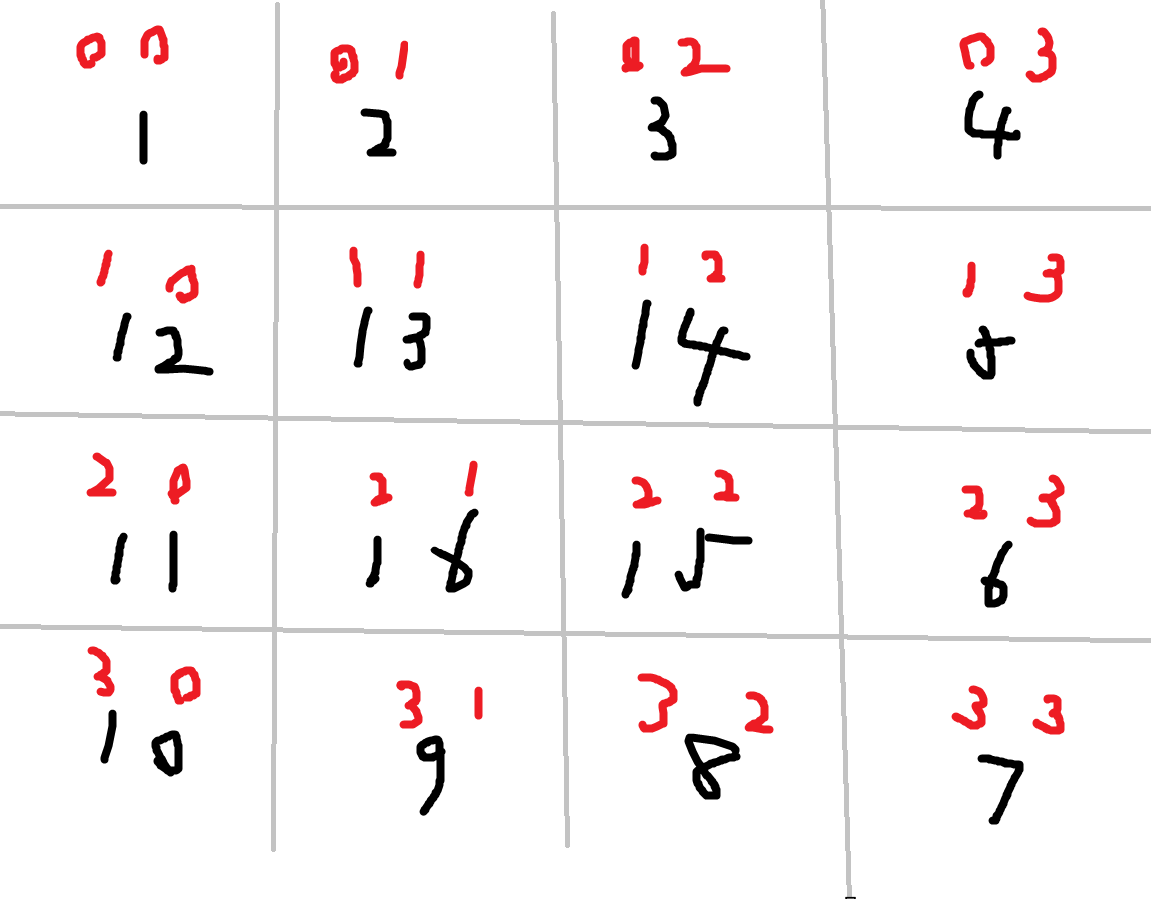
我们来寻找规律,假设坐标为(x,y)

1. 左上往右上: x不变 y++
2. 右上到右下: y不变 x++
3. 右下到左下: x不变 y–
4. 左下到左二: y不变 x–

之后就开始循环,走过的不再走

因此我们就要想怎么建立这一次循环

1. 先给矩阵定上下左右界以便后面操作

   int left=0,right=n-1,up=0,down=n-1;

2. 循环停止时,其实就是数值走到n*n了,我们设个计数器cnt

   int cnt=1;

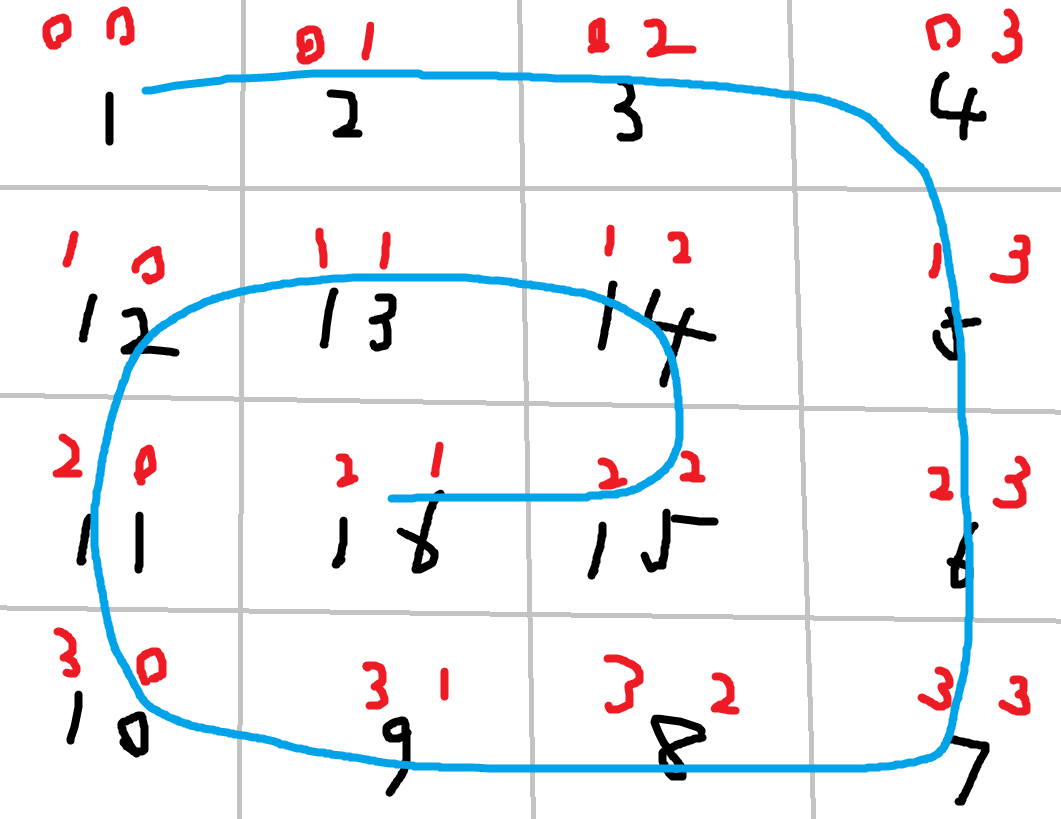
3. 思考一次循环的细节

   

   从(0,0)--->(0,3),左边界到右边界,行数==up
   for(int i=left;i<=right;i++)
   {
   	matrix[up][i]=cnt;
   	cnt++;//让每个位置匹配它所对应的值
   }
   //这里最顶上已经走完了,因此我们让up++,以便下一次循环
   up++;

   从(0,3)--->(3,3),右上到右下,因为(0,3)走过了,因此其实是
   从(1,3)--->(3,3),也就是列数==right
   for(int i=up,i<=down;i++)
   {
   	matrix[i][right]=cnt;
   	cnt++
   }
   right--;

   之后就是以此类推
   右下到左下:
    for(int i=right;i>=left;i--)
           {
               matrix[down][i]=cnt;
               cnt++;
           }
           down-=1;
           
    左下到左二
     for(int i=down;i>=up;i--)
           {
               matrix[i][left]=cnt;
               cnt++;
           }
           left+=1;

   这样一次循环就结束了,还是用4*4的来看,下一次循环由于我们把边界也变化了,因此它能够顺利地进行完全,直到cnt==n*n

4. 最终代码:

   int** generateMatrix(int n, int* returnSize, int** returnColumnSizes) {
       int ** matrix=(int **)malloc(n*sizeof(int *));
       *returnColumnSizes=(int *)malloc(n*sizeof(int));
       *returnSize=n;
   
       for(int i=0;i<n;i++)
       {
           matrix[i]=(int*)malloc(n*sizeof(int));
           (*returnColumnSizes)[i]=n;
       }
   
       int cnt=1;
       int left=0,right=n-1,up=0,down=n-1;
       while(cnt<=n*n)
       {
           for(int i=left;i<=right;i++)
           {
               matrix[up][i]=cnt;
               cnt++;
           }
           up+=1;
   
           for(int i=up;i<=down;i++)
           {
               matrix[i][right]=cnt;
               cnt++;
           }
           right-=1;
   
           for(int i=right;i>=left;i--)
           {
               matrix[down][i]=cnt;
               cnt++;
           }
           down-=1;
           
           for(int i=down;i>=up;i--)
           {
               matrix[i][left]=cnt;
               cnt++;
           }
           left+=1;
       }
       return matrix;
   
   }

   java代码

   java可以直接int[n] [n]很好用

   public int[][] generateMatrix(int n) {
           int maxNum=n*n;
           int[][] matrix=new int[n][n];
           int left=0,right=n-1,up=0,down=n-1;
           int cnt=1;
           while (cnt<=n*n) {
               for(int i = left; i <= right; i++) {
                   matrix[up][i]=cnt;
                   cnt++;
               }
               up++;
               for(int i = up; i <= down; i++) {
                   matrix[i][right]=cnt;
                   cnt++;
               }
               right--;
               for(int i = right; i >= left; i--) {
                   matrix[down][i]=cnt;
                   cnt++;
               }
               down--;
               for(int i = down; i >= up; i--) {
                   matrix[i][left]=cnt;
                   cnt++;
               }
               left++;
           }
           return matrix;
       }