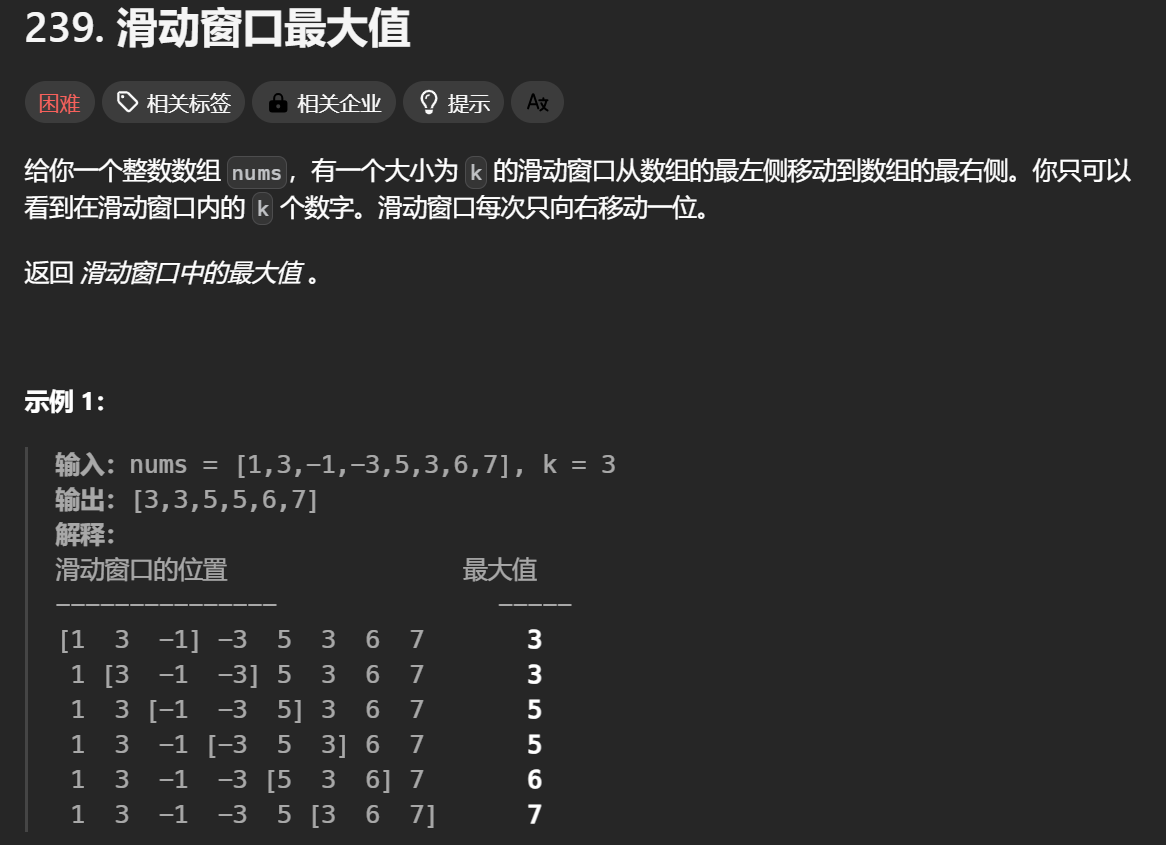
image-20241107143714400

思路

这题解的思路真的很巧妙,它使用了单调队列(满足单调性的双端队列),也就是它可以从队头或队尾插入或删除,并且他是从大到小排的

它的代码也没有多复杂,用数组就可以实现

先定义一个下标数组q ,用来存储下标方便后面操作,还有一个结果数组,用来return结果,不难通过观察发现结果的数量为numsSize-k+1

1
2
3
int q[numsSize];
*returnSize=0;
int *ans=malloc(sizeof(int)*(numsSize-k+1));

在来两个指针left和right指向他的头和尾

1
int left=0;int right=0;

  • 开始:

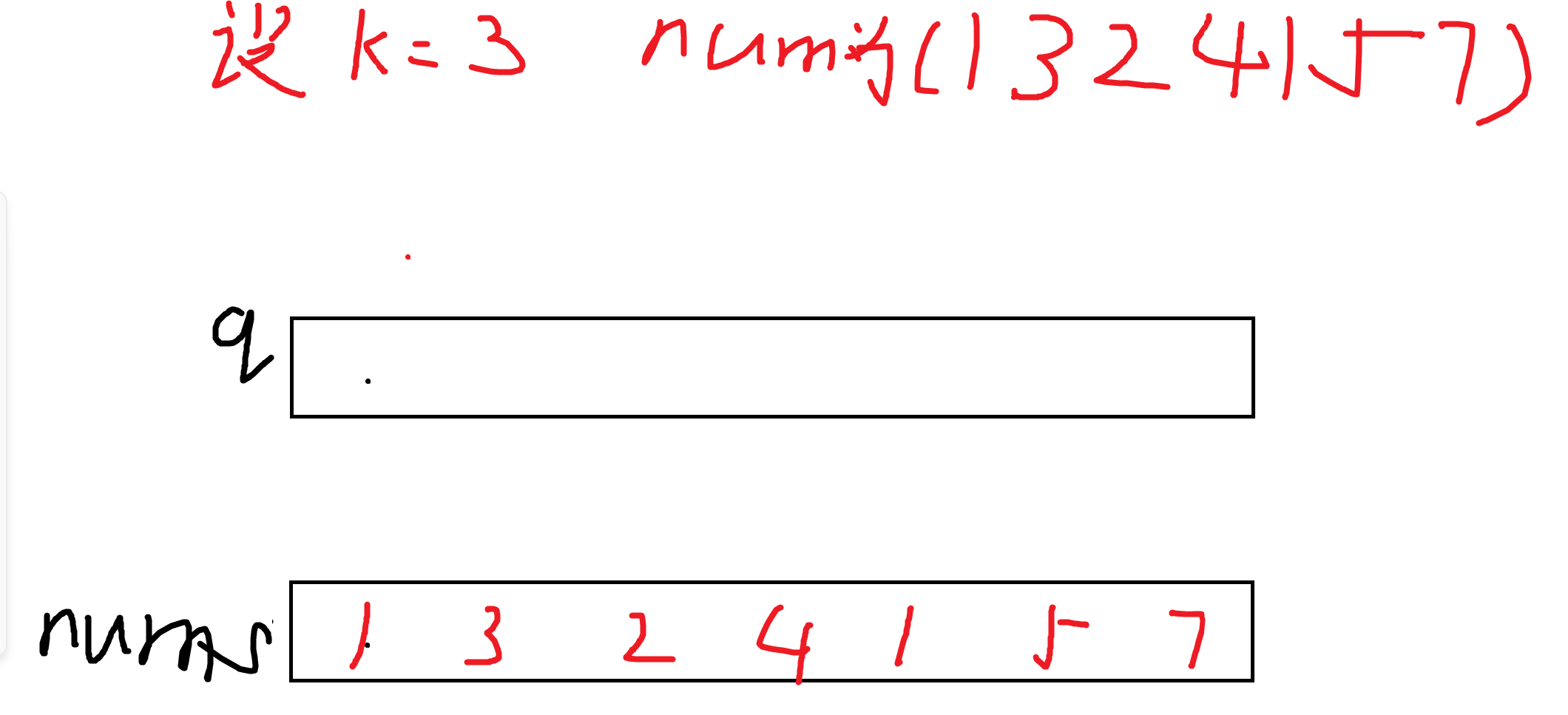
    image-20241107164839337

  • 我们先把nums里的数的下标开始一位一位的存进去,循环k次,如果后面的比前面的大,把前面的移除,来保证num[q[left]]一定是最大的从而保证递减性

    1
    2
    3
    4
    5
    !!! 如何移除:
    		当q不为空,并且nums[q[right]]<nums[i]
    		我们直接让right--
    		然后再看 q[right++]=nums[i];
    		这样就成功把前面的移除了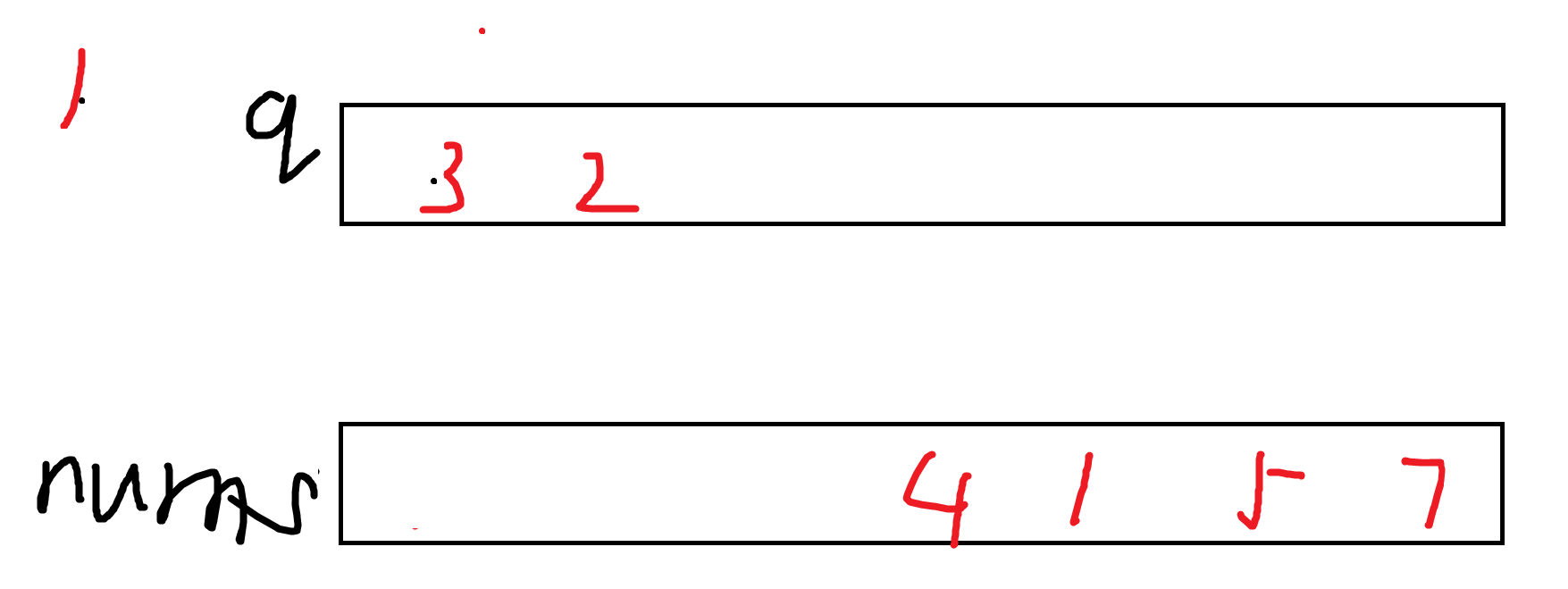
    image-20241107165129370

  • 之后先将nums[q[left]]的值存入ans中

    1
    ans[(*returnSize)++]=nums[q[left]];

  • 最后的循环:

    依然是第二步当后面比前面大的时候,把前面t了,但是由于需要滑动窗口的存在,我们不可能让原来的大的永远占住那个坑,需要找一个条件,当滑动窗口里的内容为k时把left踢了

    1
    2
    3
    4
    5
    6
    7
    8
    由于q[left]是下标,而我们遍历到了i,也就是
    (记住,一个数组两个位置下标之差+1,才是这两个下标之间(包括在内)有多少个)
    ------>i-q[left]<k;
    ------>i-k<q[left];
    ------>q[left]>i-k;
    此时不要踢出left
    也就是踢出的条件就是
    ------>q[left]<=i-k;

    之后存入ans中就ok了

  • 代码:

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    int* maxSlidingWindow(int* nums, int numsSize, int k, int* returnSize) {
        int q[numsSize];
        int left=0;int right=0;
        for(int i=0;i<k;++i){
            while(left<right&&nums[i]>nums[q[right-1]]){
                right--;
            }
            q[right++]=i;
        }
        *returnSize=0;
        int *ans=malloc(sizeof(int)*(numsSize-k+1));
        ans[(*returnSize)++]=nums[q[left]];
        for(int i=k;i<numsSize;++i){
            while(left<right&&nums[i]>nums[q[right-1]]){
                right--;
            }
            q[right++]=i;
            while(q[left]<=i-k){
                left++;
            }
            ans[(*returnSize)++]=nums[q[left]];
        }
        return ans;
    }